NEWS

- 総合
- 小学校
- 中学校
- 高校
- 特別支援学校
おすすめの「ICT 活用授業の優良事例」

学校法人別府大学明星小学校5年の総合的な学習の時間
修学旅行の班別自主研修の計画を立てよう
- #路面電車地図カード
- #データチャート
- #研修先カード
- #ロイロノート
- #iPad

学校法人別府大学明星小学校5年の理科
流れる水の働きと土地の変化
- #データチャート改良版
- #提出箱
- #ロイロノート
- #iPad

学校法人別府大学明星小学校3年の総合的な学習の時間
温泉博士になろう
- #PMIシート
- #ロイロノート
- #iPad

学校法人別府大学明星小学校1年の生活科
みんなで遊ぼう 〜「あきまつり」の招待状を考えよう〜
- #クラゲチャート
- #提出箱
- #ロイロノート
- #iPad

学校法人別府大学明星小学校5年の社会科
工業生産とわたしたちのくらし
- #熊手チャート
- #シンキングツール
- #ロイロノート
- #iPad

玖珠町立塚脇小学校6年の社会
江戸幕府による大名支配
- #Google Slides
- #Chromebook
- #Google Forms
- #Google Classroom

学校法人別府大学明星小学校5年の総合的な学習の時間
修学旅行の班別自主研修の計画を立てよう
- #路面電車地図カード
- #データチャート
- #研修先カード
- #ロイロノート
- #iPad

学校法人別府大学明星小学校5年の理科
流れる水の働きと土地の変化
- #データチャート改良版
- #提出箱
- #ロイロノート
- #iPad

学校法人別府大学明星小学校3年の総合的な学習の時間
温泉博士になろう
- #PMIシート
- #ロイロノート
- #iPad

学校法人別府大学明星小学校1年の生活科
みんなで遊ぼう 〜「あきまつり」の招待状を考えよう〜
- #クラゲチャート
- #提出箱
- #ロイロノート
- #iPad

学校法人別府大学明星小学校5年の社会科
工業生産とわたしたちのくらし
- #熊手チャート
- #シンキングツール
- #ロイロノート
- #iPad

玖珠町立塚脇小学校6年の社会
江戸幕府による大名支配
- #Google Slides
- #Chromebook
- #Google Forms
- #Google Classroom

玖珠町立くす星翔中学校3年の数学
関数 y=ax2 関数のグラフを使って、身の回りの問題を考える
- #Google Slides
- #Google spreadsheets
- #Chromebook
- #Google Forms
- #Google Jamboard
- #Google Classroom

佐伯市立本匠中学校3年の社会科(公民的分野)
現代社会を捉える枠組み
- #ロイロノート
豊後大野市立緒方中学校2年の特別活動(生徒会活動)
学校指定の上履きを変えてほしい~説得力のある主張で学校生活の改善を図ろう~
- #ロイロノート
- #Keynote

玖珠町立くす星翔中学校2年の英語
旅行を予定している Megan 先生に、その土地ですべきことが伝わるポスターを作ろう。
- #Google Slides
- #Google spreadsheets
- #Chromebook
- #Google Forms
- #Google Jamboard
- #Google Classroom

杵築市立山香中学校3年の数学
平方根
- #ロイロノート

玖珠町立くす星翔中学校2年の国語
群読で発信!800年の時を超えた『平家物語』
- #Google Slides
- #Google spreadsheets
- #Chromebook
- #Google Forms
- #Google Jamboard
- #Google Classroom

大分県立盲学校1年2年3年の理科
ブタの眼球の解剖実験〜「わかる」「つたえる」「つながる」ための生徒実験〜
- #Word
- #OneDrive
- #Share Point
- #PowerPoint
- #Teams

大分県立大分工業高等学校3年の課題研究
建設産業におけるDX(デジタルトランスフォーメーション)の現状と私たちの考える未来の建設産業の姿
- #Microsoft Teams
- #iPad
- #MetaMojiClassRoom

大分県立大分工業高等学校1年の機械設計
力と運動の法則(運動の量&働く力の関係)
- #iPad
- #MetaMojiClassRoom

大分県立中津北高等学校1年の地理歴史
第二次世界大戦の特徴と性格
- #iPad
- #MetaMojiClassRoom

大分県立大分東高等学校2年の農業
食中毒の原因となる細菌の特徴に応じた対策を理解する
- #Mentimeter
- #iPad
- #MetaMojiClassRoom

大分県立安心院高等学校1年の情報
問題解決とその方法 (章末確認テスト)
- #パスワード
- #Microsoft Teams
- #forms
大分県立さくらの杜高等支援学校高等部1年の情報
情報通信ネットワークとデータの活用に取り組むための指導
- #Microsoft Excel
- #教科学習
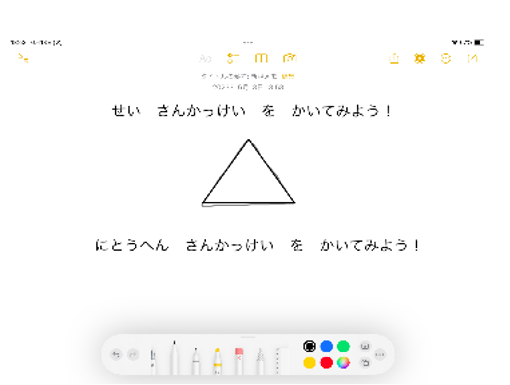
大分県立南石垣支援学校高等部2年の数学
三角形の特徴を踏まえながら作図するための指導
- #Apple Pencil
- #算数
- #知的
- #作図
- #三角形
- #図形
- #メモ
- #数学
- #iPad

大分県立新生支援学校小学部2年の図画工作科
自分や友だちの描いた作品を鑑賞するための指導・支援
- #図画工作科
- #作品鑑賞
- #iMovie
- #iPad
- #Keynote
大分県立宇佐支援学校高等部1年の登校時
1日の流れを確認し、見通しを持って活動に取り組むための支援
- #1日の流れの確認
- #iPad
- #Keynote

大分県立竹田支援学校中学部2年の国語
物語文を読んで、感じ取った登場人物の気持ちや場面の情景を表現する指導
- #読むこと
- #スイミー
- #レオ・レオニ
- #知的障がい
- #国語
- #iMovie
- #iPad
- #Keynote

大分県立別府支援学校高等部2年の自立活動
情報端末機器に慣れ、より主体的に学習に取り組むための指導
- #自律神経失調症
- #文字さがし
- #カメラ
- #Safari
- #自閉症スペクトラム
- #自己肯定感
- #自立活動
- #iPad
- #Keynote
- #zoom

全 296 件の「ICT機器等の優良活用事例」から事例をさがす
おすすめの「探究的な学びの実践事例」
※探究的な学びの実践は高等学校からです

大分県立中津東高等学校
日本の伝統芸能「落語」への挑戦

大分県立中津東高等学校
エコ電カーの製作を通して

大分県立中津北高等学校
フッ素の働き

大分県立中津北高等学校
マルコフ連鎖による読書感想文の自動生成

大分県立中津北高等学校
保育士疑似体験をして気付いた日本の保育の現状

大分県立中津南高等学校1年
やさしい日本語で異文化交流【B】 〜中津市の外国人が受診しやすい医療環境〜

全 15 件の「探究的な学びの実践事例」から事例をさがす
- ニュース
- 新着情報
GIGAスクールインタビュー記事を公開しました。
ICT活用事例実践者へのインタビュー動画を4本公開しました。
インタビュー動画を公開しました。(大分県立別府支援学校)
インタビュー動画を公開しました。(玖珠町立くす星翔中学校)
ICT活用事例を追加しました
ICT活用授業&探究ライブラリポータルサイト開設!
一般競争入札のお知らせ(ネットあんしんセンター運営業務委託)
活用型情報モラル教材「GIGAワークブックおおいた」
公募型企画提案競技の実施のお知らせ【令和6年度県立高校全国募集周知等委託業務(大分県立安心院高等学校)】
「おおいた文化財ずかん」を公開しました!
令和7年度大分県公立学校教員採用選考試験(令和6年度実施)
令和6年度 第2回教育委員会会議